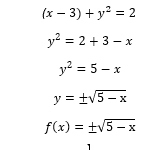المقدمة
علم الجبر الجامعي هو فرع من فروع الرياضيات
يهتم بدراسة البنى الجبرية مثل المجموعات والحلقات والحقول والفضاءات والمتجهات والأعداد المركبة والمصفوفات. يهدف علم الجبر إلى فهم الخواص الأساسية لهذه البنى
وكيفية تفاعلها مع العمليات الرياضية المختلفة.(العلي،2023م)
الدالة في الرياضيات هي مفهوم يشبه آلة تأخذ
مدخلات وتنتج مخرجات بناءً على علاقة معينة. هذه العلاقة تربط بين مجموعتين:
المجموعة الأولى تُسمى المجال، والتي تحتوي على جميع المدخلات الممكنة، والمجموعة
الثانية تُسمى المجال المقابل أو المدى، والتي تحتوي على جميع المخرجات الممكنة.(معلا،2022م)
تتميز الدالة بأن كل عنصر في المجال يرتبط
بعنصر واحد فقط في المجال المقابل. لا يمكن لأي عنصر في المجال أن يرتبط بأكثر من
عنصر في المجال المقابل.
المدى هو مجموعة القيم الفعلية التي تنتجها
الدالة. يجب التمييز بين المجال والمدى، فقد لا تشمل الدالة جميع قيم المجال
المقابل، فيكون المدى في هذه الحالة مجموعة جزئية من المجال المقابل.
بالنظر للعلاقة:
(x-3)+y^2=2
● هل تمثل هذه العلاقة دالة (مع ذكر السبب) ؟
، الدالة هي عبارة عن علاقة ربط بين
متغيرين حيث يكون لكل قيمة من المتغير الأول قيمة واحدة محددة للمتغير الثاني.
بمعنى آخر، إذا كان لكل قيمة x
هناك قيمة y واحدة فقط مرتبطة بها،
فإن العلاقة تُصنف كدالة.
في حالة العلاقة (x-3)+y^2=2، عند تحويلها إلى صيغة y=f(x) قد نجد مشكلة. عند حل المعادلة للحصول على y، سنحصل على معادلة دائرية بدلاً من مُعادلة
توضّح علاقة واضحة بين x
و y. بمعنى آخر، لكل قيمة x يمكن أن يكون هناك قيمتين مختلفتين لـ y تتوافقان مع المعادلة، وهذا يعني أنها ليست
دالة.
وهذا يُظهر الفرق بين الدوال والعلاقات
الأخرى في الرياضيات، حيث أن الدوال تكون علاقات توضح تأثير واحد من متغيرين على
الآخر بشكل واضح ومحدد، بينما العلاقات الأخرى قد تحتوي على قيم متعددة ومتناقضة
لنفس المتغير.
سأقوم بتحويل العلاقة إلى دالة :
وعلى الرسم البياني، يمكن تمثيل ذلك بهذه الطرقة:
النطاق أو المجال عبارة
عن:[5,∞− ]
والمدى يكون بهذه
الطريقة : [+∞,0]
بالإضافة إلى التعبير عن x
كدالة في صورة y سأقوم بالتالي : x = g(y)
الرسم البياني
 |
بالتالي يكون المجال او
النطاق : (+∞,-∞) المدى يكون بهذه الطريقة (5 ,-∞) |
اشرح
ماذا تمثل النقط ( (2,1) (4,1, ( (3,0 ((1,0 لهذه العلاقة ثم أوجد تقاطع
هذه العلاقة مع محاور الإحداثيات.
كما
نلاحظ، عند التعويض بالنقاط المعطاة لإيجاد نقاط التقاطع، حدث التقاطع في النقطة ( (4,1، حيث تساوى الناتج مع المعادلة.
 |
| الرسم البياني |
ختامًا،
يأتي دور الجبر بأهمية حيوية في التطور العلمي والتكنولوجي، حيث يساهم بشكل فعال
في فهم العلاقات الرياضية وتحليلها. يسهل الجبر فهم العلاقات المعقدة ويبسطها، مما
يساعد في التفكير التحليلي وحل المشكلات بطرق مبتكرة. لذا، من الضروري فهم أساسيات
الجبر وتطبيقاتها لتحقيق النجاح في مجالات الرياضيات والتخصصات الأخرى التي تخدم
مستقبلنا وتعزز فهمنا للعالم من حولنا.
المراجع:
العلي،
براءة.(2023م) . ما هو علم الجبر في الرياضيات، موقع
موضوع. تم الاسترجاع
من الرابط: https://n9.cl/6bnyq
معلا
، جود. (2022م) تعريف الدوال، موقع مرسال. تم الاسترجاع من الرابط:
إعداد : فريق المنارة
للتعليم الجامعي